|
| |
Key Predictive Dynamix Modeling Algorithms
 Regression Models |
Regression models have been the mainstay of predictive modeling for
many decades. Linear regression models characterize the
relationship between inputs and outputs using a linear equation (y
=
SXiWi
+ c) with one coefficient per input. Regression
coefficients are determined via a least squares algorithm to minimize
error across the training dataset. Because there is a single weight
per input linear regression models are easily interpreted but cannot
represent non-linear relationships and interactions between inputs.
In order to extend the capabilities of regression models,
non-linear transformations are often applied to the model inputs or
outputs (i.e., logistic regression, polynomial regression, etc.). |
 Neural Networks |
Modern neural network technology are powerful computational
structures for solving difficult problems involving forecasting and
pattern recognition.
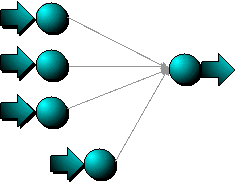
Multi-layer perceptron neural networks have an architecture that allows
multiple coefficients per input variable. The processing at each node
is functionally equivalent to logistic regression. Multiple nodes
(organized into layers) allow the model to represent complex,
non-linear, interactions between variables.
Neural networks address issues of information overload by distilling
many variables into actionable decisions. By discovering
underlying patterns and trends in data, neural nets arrive at decisions
without requiring you to specify the form of the model. Neural
networks have been described as “universal approximators.” This
term comes from the fact that they have proven capable of accurately
approximating any functional relationship regardless of complexity. |
 Clustering & Segmentation |
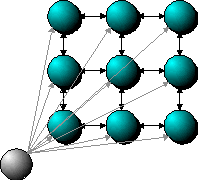
Clustering networks add an important dimension to any data analysis
effort. They are easy to use and extremely flexible. Because of
their lattice structure, they can effectively map high dimensionality
vectors (i.e., many variables) into a smaller number of dimensions.
This provides an excellent structure for preprocessing and visualizing
data. They are also used for dataset sampling, outlier detection,
and input validation for other types of models.
Clustering models use a form of unsupervised, competitive learning.
They are “unsupervised” in that there is no “right” answer provided in
order to train the model. Instead, the model wraps itself around
the dataset in order to provide coverage across the entire distribution
of data. When a new data point is provided to the model, all of
the nodes compete for it. During training, the closest node wins and is
adjusted closer to the data point. After training, nodes are no
longer adjusted and winning nodes are used for classification of the
incoming data points. |
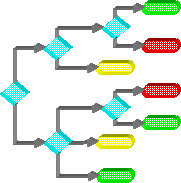 Decision Trees |
Decision
trees use hierarchical, joint variable conditions to break-up a solution
space into subspaces. These conditional sub-spaces can then be used to
classify input patterns or forecast output values. They are called
trees due to the hierarchical node/link flowchart-type graph that is
often used to depict the various conditional decision paths. Tree
leaf nodes can be interpreted as IF-THEN rules where each link leading
into the node represents a set of AND-ed conditions (ex., IF iVar1=a and
iVar2=b and iVar3=c THEN oVar = d).
Decision trees train by selecting the most
discriminative variable from the list of candidate variables then
recursively selecting the most discriminative variable for each branch
(i.e., possible value) of the previous variable. Training stops
when the are no further variables can be added to improve classification
accuracy or tree branches become overly specific (i.e., cover too few
cases). |
 Fuzzy Logic |
Fuzzy logic provides an intuitive, rule-based means for
expressing continuous-valued or proportional relationships between variables.
Variable values are defined to fall within membership functions to a
greater or lesser degree (Ex., Container is Empty, Price is High,
Inventory is Low). Fuzzy IF-THEN rules use logical operators to combine
joint variable memberships to express continuous, logical rule behavior.
When a fuzzy system is executed, every rule fires...but only to the
degree that each rule's premise is true. Many rules may be true to
degree 0, thus, have no effect on the outcome.
Fuzzy logic is a fit for problems where there is
a good understanding of the system's dynamics such that meaningful rules
can be written, even if they are imprecise. Once the rules are
defined, rule weights can be tuned with available
data. Because variable memberships can overlap with one another,
fuzzy systems can be more
robust than crisp
rule-based approaches. |
 Genetic Algorithms |
Genetic algorithm technology is a powerful
optimization method. It’s name comes from the use of genetically
analogous search operators such as cross-over and mutation, and
principles of survival of the fittest. With GA, a population of
solutions is generated and evaluated as to each solution’s
“fitness”. Then, each solution’s characteristics are
probabilistically carried over into the next generation based on how
well it solves the problem.
GA technology has proven to be a very
powerful generalized optimization method. It is extremely flexible
and can be used to optimize complex computational structures.
|
For more information see technical whitepapers.
|